Introduction

Pull-out tests of fibers from composites are important methods to determine the composite properties. Different mechanical models have been developed in order to predict the stress distribution in the composite in such tests. Examples for early works are the articles by Cox [12] and Rosen [41]. The single-fiber pull-out test has been modeled in different works such as Fu et al. [18] and Kim et al. [33]. This single-fiber shear-lag might also be useful as a representative volume element for an array of parallel fibers of equal geometric and mechanical properties (see, e.g., Lenci and Menditto [35], Meng and Wang [37], and Upadhyaya and Kumar [45]).

The bonding conditions between two constituents have a crucial role in the functionality of composites, and an understanding of the development of the mechanical properties with ongoing damage processes guarantees an efficient use of this class of materials. Interfacial bonding between constituents is formed by different mechanisms such as molecular entanglement which is then followed by inter-diffusion, electrostatic attraction, chemical reaction, or mechanical keying [15]. In many cases the fibers in polymer matrices are surface-treated or coated by an interphase to improve the adhesion between the constituents mechanically of chemically (see, e.g., Wu et al. [46]), and Karger-Kocsis et al. [32] review the recent developments in fiber/matrix interphase engineering for polymer composites. In mechanical modeling, a single interphase layer or a multitude of interphase layers might simulate a graded or degraded part of the matrix (see, e.g., Fomenko et al. [17], and Andrianov et al. [4]), which might, for example, be the result of exposure to environmental conditions such as air or moisture. Yao et al. [47] present a modified shear-lag model that considers a graded interphase with varying Young's modulus in the radial direction. Different developments in the analytic modeling of fiber pull-out problems are treated in the recent book by Andrianov et al. [2]. Andrianov et al. [2] study different two-dimensional problems of axially loaded, coated and uncoated fibers, and they discuss that these results can be generalized in order to be applied for three-dimensional problems.

Imperfect bonding might be the result from numerous factors such as cracks, corrosion, or degradation of the material [20]. Different approaches have been developed in order to model imperfect bonding between two constituents. A popular model is denoted as the spring-layer model, which has been proposed in the work by Goland and Reisner [23]. Examples of works that apply the spring-layer model are the articles by Geymonat et al. [21], Krasucki and Lenci [34], Nazarenko et al. [39], and Golub and Doroshenko [24]. The works by Danishevskyy et al. [13] and Andrianov et al. [6] consider a nonlinear spring-layer modeled in their modeling of imperfect bonding. The spring-layer model shows analogies to the thermal resistance models [3, 7]. A model that describes piece-wise varying bonding conditions in the circumferential orientation along the fiber surface has been used in [36] in the context of the calculation of the effective shear stiffness of periodic fibrous composites. A popular alternative for modeling imperfect bonding is to introduce an artificial layer between two constituents. The thickness of such a modeling layer is considerably smaller than the diameter of the fiber, and the geometric and mechanical properties of such an artificial layer define the bonding quality. This idea has been applied in different works such as Hashin [26], Benveniste and Miloh [9] and Sevostianov et al.  [42]. Andrianov et al. [5] compare the spring-layer model to the artificial layer approach in order to estimate the quality of artificial layer method. The latter approach may then be applied to problems where boundary conditions may not be taken into account explicitly. When the pull-out forces are large enough, the fibers will slide or even tear. Hutchinson and Jensen [31] study axially loaded fibers, and they consider friction between the fibers and the matrix. Partial and full interfacial debonding of fibers in pull-out tests has been modeled in different works, for example in a series of articles by Hsueh [27, 28] and by Chang et al. [10].

In many industrial applications, the matrix constituent is made of polymers, which often reveal a viscoelastic behavior for the considered time interval of loading. At the same time, the time-dependent behavior of the fibers is often taken to be negligibly small. Based on observations from fiber pull-out tests, the modeling work by Hsueh [29] takes into account a viscous interphase layer between the fibers.

Time-dependent mechanical behavior of the material is often modeled in terms of a combination of springs, which represent an elastic behavior, and dashpots, which represent a viscous behavior. The elastic–viscoelastic correspondence principle is based on the idea that the treatment of the linear elastic problem and the Laplace transformed viscoelastic problem shows certain analogies (see, e.g., the classical book by Flügge [16]). This principle has been applied in different works, for example by Hashin [25] and by Reza and Shishesaz [40], on composites. Andrianov et al. [8] applied this principle in order to study planar load transfer problems for fibers that are pulled out of a viscoelastic matrix.

The present work generalizes previous works in the field of fiber pull-out modeling, and bonding between the fiber and interphase layer, and between an interphase layer and the matrix is taken to be imperfect. The quality of bonding is modeled to vary in the axial direction. While the bonding quality in the contact interfaces between two constituents is often taken to be constant, this work assumes that the bonding strength may be relatively low near the surface of the composite, where the material is subjected to different environmental conditions, and the bonding strength may increase along the axial fiber direction with the distance from the surface. In the different contact surfaces, the bonding quality may differ, i.e., the bonding may still be intact in one interface, for example between the fiber and the interphase, but imperfect in another interface, for example between the interphase and the matrix. In addition to the time-independent elastic treatment, this article also studies the local stress distribution in the material for a viscoelastic behavior of the matrix. The interplay of the viscoelastic behavior and imperfect bonding is then studied in some numerical results. Special cases of our herein presented model are then compared to known results from the literature.

This article is organized as follows: Sect. 2 describes the fiber pull-out problem, where axially varying bonding conditions between the fiber and its coating and between the coating and the matrix are taken into account. Section 3 studies the distribution of the stresses in the composite, and it provides some numerical examples that illustrate the impact of the bonding conditions on these stress distributions. Viscoelastic behavior of constituents is then studied in Sect. 4, and some numerical examples study the development of the stress distribution with creep and relaxation. The final Sect. 5 presents some conclusions.

Fig. 1
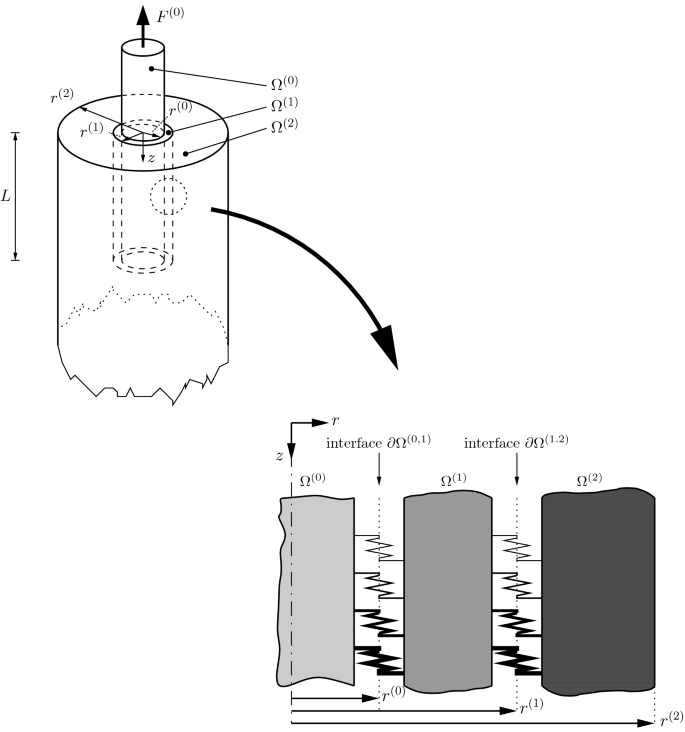
figure 1

Cylinder model of the composite, which consists of a fiber \(\varOmega ^{(0)}\) in the center, the interphase \(\varOmega ^{(1)}\), and the matrix \(\varOmega ^{(2)}\). The bonding between the constituents is taken to be imperfect and varying with the axial coordinate z. The force \(F^{(0)}\) must be balanced in order to avoid displacement of the cylinder as a rigid whole. This force is in balance with the force \(\varSigma _{zz}^{(2)}(L)A^{(2)}\) that results from the average normal stresses \(\varSigma _{zz}^{(2)}(z)\) at the axial location \(z=L\) over the cross-sectional area of the matrix

Full size image

Pulled-out fibers

Figure 1 shows an elastic fiber \(\varOmega ^{(0)}\) in the center of a cylinder, which is also denoted as the double shear-lag model [30]. The fiber is subjected to a force \(F^{(0)}\) in the axial direction, which tends to pull the fiber out. This fiber has the length L, the Young's modulus \(E^{(0)}\), the shear modulus \(\mu ^{(0)}\), the radius \(r^{(0)}\), and the cross-sectional area \(A^{(0)}=\pi \left[ r^{(0)}\right] ^2\). This fiber is coated by a material \(\varOmega ^{(1)}\) with the Young's modulus \(E^{(1)}\), the shear modulus \(\mu ^{(1)}\), the thickness \(r^{(1)}-r^{(0)}\), and therefore with the cross-sectional area \(A^{(1)}=\pi \{\left[ r^{(1)}\right] ^2-\left[ r^{(0)}\right] ^2\}\). This constituent \(\varOmega ^{(1)}\) may represent an interphase, such as a coupling agent, or it may be used as a thin (\(r^{(1)}-r^{(0)}\ll r^{(0)}\)) modeling layer. This coated fiber is embedded in a matrix \(\varOmega ^{(2)}\) with the Young's modulus \(E^{(2)}\), the shear modulus \(\mu ^{(2)}\), the thickness \(r^{(2)}-r^{(1)}\), and therefore with the cross-sectional area \(A^{(2)}=\pi \{\left[ r^{(2)}\right] ^2-\left[ r^{(1)}\right] ^2\}\).

The shear stress \(\tau ^{(i)}_{rz}(r,z)\) in the constituent \(\varOmega ^{(i)}\), \(i=0, 1,2\), is related to the axial displacements \(u^{(i)}_{z}(r,z)\) through the shear modulus \(\mu ^{(i)}\), and the axial normal stress \(\sigma ^{(i)}_{zz}(r^{(i)},z)\) is related to the axial displacements \(u^{(i)}_{z}(r^{(i)},z)\) through the Young's modulus \(E^{(i)}\):

$$\begin{aligned} \tau ^{(i)}_{rz}(r,z)= & {} \mu ^{(i)}\dfrac{\partial u^{(i)}_{z}(r,z)}{\partial r},\qquad i=0, 1,2, \end{aligned}$$

(1a)

$$\begin{aligned} \sigma ^{(i)}_{zz}(r,z)= & {} E^{(i)}\dfrac{\partial u^{(i)}_{z}(r,z)}{\partial z},\qquad i=0, 1,2. \end{aligned}$$

(1b)

The bonding between the constituents may be imperfect. We assume that bonding may vary with the axial location z, for example because bonding might be affected by environmental conditions such as air or moisture.

Consider bonding between the fiber \(\varOmega ^{(i-1)}\) and its neighboring phase \(\varOmega ^{(i)}\) to be imperfect and to be described by the spring-layer model. In this spring-layer model, in the interface \(\partial \varOmega ^{(i-1,i)}\) between \(\varOmega ^{(i-1)}\) and \(\varOmega ^{(i)}\) the shear stresses \(\tau ^{(i-1)}_{rz}(r^{(i-1)},z)\) and \(\tau ^{(i)}_{rz}(r^{(i-1)},z)\) are equal, while the differences in the axial displacements \(u^{(i-1)}_{rz}(r^{(i-1)},z)\) and \(u^{(i)}_{rz}(r^{(i-1)},z)\) are proportional to the shear stresses:

$$\begin{aligned}&\tau ^{(i-1)}_{rz}(r^{(i-1)},z)=\tau ^{(i)}_{rz}(r^{(i-1)},z), \end{aligned}$$

(2a)

$$\begin{aligned}&u^{(i)}_{z}(r^{(i-1)},z)-u^{(i-1)}_{z}(r^{(i-1)},z)=\gamma ^{(i-1,i)}(z) \; \tau ^{(i-1)}_{rz}(r^{(i-1)},z). \end{aligned}$$

(2b)

The parameter \(\gamma ^{(i-1,i)}(z)\) in Eq. (2b) is the bonding factor, which quantifies the bonding quality. Let us now differentiate Eq. (2b) with respect to z by the application of the product rule:

$$\begin{aligned}&\dfrac{\partial u^{(i)}_{z}(r^{(i-1)},z)}{\partial z} - \dfrac{\partial u^{(i-1)}_{z}(r^{(i-1)},z)}{\partial z} = \dfrac{\partial \gamma ^{(i-1,i)}(z)}{\partial z}\tau ^{(i-1)}_{rz}(r^{(i-1)},z) \nonumber \\&\quad \quad + \gamma ^{(i-1,i)}(z)\dfrac{\partial \tau ^{(i-1)}_{rz}(r^{(i-1)},z)}{\partial z}. \end{aligned}$$

(3)

Note that in Eqs. (2) and (3) \(r^{(-1)}=0\) would refer to the axis of the fiber, in which \(\tau ^{(-1)}_{rz}=0\). Using the relation between the axial displacement and the normal axial stress in (1b), we can express the normal stress \(\sigma ^{(1)}_{zz}(r^{(0)},z)\) and \(\sigma ^{(2)}_{zz}(r^{(1)},z)\) as

$$\begin{aligned} \sigma ^{(1)}_{zz}(r^{(0)},z)= & {} \dfrac{E^{(1)}}{E^{(0)}}\sigma ^{(0)}_{zz}(r^{(0)},z)+ E^{(1)}\dfrac{\partial \gamma ^{(0,1)}(z)}{\partial z}\tau ^{(0)}_{rz}(r^{(0)},z)+ E^{(1)}\gamma ^{(0,1)}(z)\dfrac{\partial \tau ^{(0)}_{rz}(r^{(0)},z)}{\partial z}, \end{aligned}$$

(4a)

$$\begin{aligned} \sigma ^{(2)}_{zz}(r^{(1)},z)= & {} \dfrac{E^{(2)}}{E^{(1)}}\sigma ^{(1)}_{z}(r^{(1)},z)+ E^{(2)}\dfrac{\partial \gamma ^{(1,2)}(z)}{\partial z}\tau ^{(1)}_{rz}(r^{(1)},z)+ E^{(2)}\gamma ^{(1,2)}(z)\dfrac{\partial \tau ^{(1)}_{rz}(r^{(1)},z)}{\partial z}. \end{aligned}$$

(4b)

Note that special cases of the herein presented model lead to known models that have been studied in other research works. If \(\gamma ^{(0,1)}(z)=\gamma ^{(1,2)}(z)=0\) so that bonding is the interface is in perfect contact with both the fiber and the matrix, then Eqs. (2) reduce to \(\tau ^{(0)}_{rz}(r^{(0)},z)=\tau ^{(1)}_{rz}(r^{(0)},z)\) and \(u^{(0)}_{z}(r^{(0)},z)=u^{(1)}_{z}(r^{(0)},z)\) for \(i=1\) and to \(\tau ^{(1)}_{rz}(r^{(1)},z)=\tau ^{(2)}_{rz}(r^{(1)},z)\) and \(u^{(1)}_{z}(r^{(1)},z)=u^{(2)}_{z}(r^{(1)},z)\) for \(i=2\) (see, e.g., [30]). In a fiber–matrix composite in the absence of an interphase layer, different works such as the article by Lenci and Menditto [35] apply the spring-layer model for a constant bonding factor, which would correspond to our \(\gamma ^{(0,1)}\) or \(\gamma ^{(1,2)}\) in a z-independent and constant specification.

We assume that the diameter of the fiber is small in comparison with the diameter of the cylinder model, and the stiffness of the fiber is much larger than the stiffness of the other constituents, so that in Eq. (4a) we may write \(\varSigma ^{(0)}_{zz}(z)=\sigma ^{(0)}_{zz}(r^{(0)},z)=\frac{F^{(0)}}{A^{(0)}}\), where \(\varSigma ^{(0)}_{zz}(z)\) is the average normal stress in the fiber which just depends on the axial coordinate z.

The outer surface of the cylinder is taken to be free from shear stresses:

$$\begin{aligned} \tau ^{(2)}_{rz}(r^{(2)},z)=0. \end{aligned}$$

(5)

The boundary condition (5) may result from different considerations. As a first example, consider the case that the cylinder model in Fig. 1 represents a single-fiber model, and this cylinder is not in contact with any other material at the outer surface in the radial direction. Then, condition (5) results from the general assumption of stress freedom at the model's outer surface [18, 30, 37]. As a second example, consider an array of parallel fibers of equal geometric and mechanical properties, which are equally loaded by a pull-out force. Then, such a cylinder model in Fig. 1 can be treated as a representative volume element [35, 37, 45].

In our modeling we assume that in the location \(z=L\) in the axial direction there is no contact between the fiber and the matrix and between the interphase and the matrix.

Stress distribution in the composite

In order to find the relation between \(F^{(0)}\) and the stress distribution, we will first derive a relation between the average normal stresses of a constituent and the interfacial shear stresses at the boundaries of this component. In the second step, the relation between the pull-out force \(F^{(0)}\) and the average normal stresses is determined. In the third part of this section, we then obtain a system of coupled ordinary differential equations in terms of the average normal stresses, and the solution of this system gives a detailed distribution of the different stresses in the cylinder model.

Relation between interfacial shear stresses and average normal stresses

The forces that result from the average normal stresses in the different constituents are in balance with the pull-out force \(F^{(0)}\). In order to determine the average normal stresses in the fibers, we need to find a relation between the shear stresses in the interfaces and the average normal stresses. For the shear stresses \(\tau ^{(i)}_{zz}\) in the interphase \(\varOmega ^{(1)}\) and in the matrix \(\varOmega ^{(2)}\) of the unit cell, we take ansatzes in the forms (see, e.g., [18, 30])

$$\begin{aligned} \tau ^{(i)}_{rz}(r,z)=\dfrac{a^{(i)}(z)}{r}+b^{(i)}(z)r,\qquad i=1,2, \end{aligned}$$

(6)

where \(a^{(i)}=a^{(i)}(z)\) and \(b^{(i)}=b^{(i)}(z)\) are parameters, which depend on the axial coordinate z. These parameters have the forms

$$\begin{aligned} a^{(i)}(z)= & {} \tau ^{(i)}_{rz}(r^{(i-1)},z) B_1^{(i)} + \tau ^{(i)}_{rz}(r^{(i)},z) B_2^{(i)}, \end{aligned}$$

(7a)

$$\begin{aligned} b^{(i)}(z)= & {} \tau ^{(i)}_{rz}(r^{(i-1)},z) B_3^{(i)} + \tau ^{(i)}_{rz}(r^{(i)},z) B_4^{(i)}, \end{aligned}$$

(7b)

where \(B_1^{(i)}\), \(B_2^{(i)}\), \(B_3^{(i)}\), and \(B_4^{(i)}\) are four constants that result from the geometry of the cylinder model,

$$\begin{aligned} B_1^{(i)}= & {} \dfrac{\left[ r^{(i)}\right] ^2 r^{(i-1)}}{\left[ r^{(i)}\right] ^2-\left[ r^{(i-1)}\right] ^2} , \quad B_2^{(i)} = -\, \dfrac{r^{(i)}\left[ r^{(i-1)}\right] ^2}{\left[ r^{(i)}\right] ^2-\left[ r^{(i-1)}\right] ^2} , \end{aligned}$$

(8a)

$$\begin{aligned} B_3^{(i)}= & {} -\, \dfrac{r^{(i-1)}}{\left[ r^{(i)}\right] ^2-\left[ r^{(i-1)}\right] ^2}, \quad B_4^{(i)} = \dfrac{r^{(i)}}{\left[ r^{(i)}\right] ^2-\left[ r^{(i-1)}\right] ^2}. \end{aligned}$$

(8b)

The average normal stresses \(\varSigma ^{(i)}_{zz}(z)\) in the component \(\varOmega ^{(i)}\) and the shear stresses \(\tau ^{(i)}_{rz}(r^{(i-1)},z)\) and \(\tau ^{(i)}_{rz}(r^{(i)},z)\) in the interfaces \(\partial \varOmega ^{(m-1,m)}\) and \(\partial \varOmega ^{(m,m+1)}\) to the neighboring components are related via [38]

$$\begin{aligned} \dfrac{\partial \varSigma ^{(i)}_{zz}(z)}{\partial z} = \frac{2 \left[ r^{(i-1)}\tau ^{(i)}_{rz}(r^{(i-1)},z)- r^{(i)}\tau ^{(i)}_{rz}(r^{(i)},z) \right] }{\left[ r^{(i)}\right] ^2-\left[ r^{(i-1)}\right] ^2}. \end{aligned}$$

(9)

For \(i=0\) in (9,) we obtain the following relations between the interfacial shear stress and the average normal stress for the fiber,

$$\begin{aligned} \tau ^{(0)}_{rz}(r^{(0)},z)=-\dfrac{r^{(0)}}{2}\dfrac{\partial \varSigma ^{(0)}_{zz}(z)}{\partial z}. \end{aligned}$$

(10)

For \(i=2\) in (9), we obtain the following relations between the interfacial shear stress and the average normal stress for the matrix:

$$\begin{aligned} \tau ^{(1)}_{rz}(r^{(1)},z) = \dfrac{\left[ r^{(2)}\right] ^2-\left[ r^{(1)}\right] ^2}{2 r^{(1)} } \dfrac{\partial \varSigma ^{(2)}_{zz}(z)}{\partial z}. \end{aligned}$$

(11)

Equations (10) and (11) relate the shear stresses in the interfaces \(\partial \varOmega ^{(0,1)}\) and \(\partial \varOmega ^{(1,2)}\) to the average normal stresses in the fiber and in the matrix. This allows to rewrite the parameters \(a^{(i)}\) and \(b^{(i)}\) in terms of the geometric parameters and the average normal stresses.

For \(i=1\) the parameters in (7) become

$$\begin{aligned} a^{(1)}(z)= & {} C_1^{(1)}\dfrac{\partial \varSigma ^{(0)}_{zz}(z)}{\partial z} + C_2^{(1)}\dfrac{\partial \varSigma ^{(2)}_{zz}(z)}{\partial z}, \end{aligned}$$

(12a)

$$\begin{aligned} b^{(1)}(z)= & {} C_3^{(1)}\dfrac{\partial \varSigma ^{(0)}_{zz}(z)}{\partial z} + C_4^{(1)}\dfrac{\partial \varSigma ^{(2)}_{zz}(z)}{\partial z}, \end{aligned}$$

(12b)

where we have applied (10) and (11), as well as the abbreviation

$$\begin{aligned} C_1^{(1)}= & {} -\,\dfrac{r^{(0)}B_1^{(1)}}{2}, C_2^{(1)}= -\,\dfrac{1}{2}\dfrac{B_2^{(1)}}{B_3^{(1)}},\\ C_3^{(1)}= & {} -\,\dfrac{r^{(0)}B_3^{(1)}}{2}, C_4^{(1)}= -\dfrac{1}{2}\dfrac{B_4^{(1)}}{B_3^{(1)}}, \end{aligned}$$

in order to collect the geometric parameters.

For \(i=2\) the parameters \(a^{(i)}\) and \(b^{(i)}\) in (7) become

$$\begin{aligned} a^{(2)}(z)= & {} C_1^{(2)} \dfrac{\partial \varSigma ^{(2)}_{zz}(z)}{\partial z}, \end{aligned}$$

(13a)

$$\begin{aligned} b^{(2)}(z)= & {} C_3^{(2)} \dfrac{\partial \varSigma ^{(2)}_{zz}(z)}{\partial z}, \end{aligned}$$

(13b)

where we have applied (11) as well as the abbreviations

$$\begin{aligned} C_1^{(2)}=-\,\dfrac{1}{2}\dfrac{B_1^{(2)}}{B_3^{(1)}}, \qquad C_3^{(2)}=-\,\dfrac{1}{2}\dfrac{B_3^{(2)}}{B_3^{(1)}} \end{aligned}$$

for the geometric parameters.

Balance of pull-out force and the forces that result from average normal stresses

Under the condition (5), the applied external force \(F^{(0)}\) and the forces \(\varSigma ^{(i)}_{zz}(z)A^{(i)}\), which result from the averaging stresses \(\varSigma ^{(i)}_{zz}(z)\) in the different components \(\varOmega ^{(i)}\), are in equilibrium for any axial location z,

$$\begin{aligned} F^{(0)} =A^{(0)}\varSigma ^{(0)}_{zz}(z) +A^{(1)}\varSigma ^{(1)}_{zz}(z) +A^{(2)}\varSigma ^{(2)}_{zz}(z) . \end{aligned}$$

(14)

Let us assume that for \(z=0\) the fiber force is in balance with the axial fiber force, and at \(z=L\) the fiber force is in balance with the force that results from the average normal stresses in the matrix. This results in the following boundary conditions for the average normal stresses in the fiber, in the coating, and in the matrix:

$$\begin{aligned} \varSigma ^{(0)}_{zz}(0)= & {} \dfrac{F_0}{A^{(0)}},\qquad \varSigma ^{(0)}_{zz}(L)=0, \end{aligned}$$

(15a)

$$\begin{aligned} \varSigma ^{(1)}_{zz}(0)= & {} 0,\qquad \varSigma ^{(1)}_{zz}(L)=0,\end{aligned}$$

(15b)

$$\begin{aligned} \varSigma ^{(2)}_{zz}(0)= & {} 0,\qquad \varSigma ^{(2)}_{zz}(L)=\dfrac{F_0}{A^{(2)}}. \end{aligned}$$

(15c)

The average normal stresses \(\varSigma ^{(i)}_{zz}(z)\) in the component \(\varOmega ^{(i)}\) can be determined from an axial normal stresses distribution \(\sigma ^{(i)}_{zz}(r,z)\) on the cross-sectional area \(A^{(i)}\). The force \(\varSigma ^{(i)}_{zz}(z)A^{(i)}\), which results from the average normal stress \(\varSigma ^{(i)}_{zz}(z)\) in the component \(\varOmega ^{(i)}\) with the cross-sectional area \(A^{(i)}\), is equal to the force \(\int _{r^{(i-1)}}^{r^{(i)}}\sigma ^{(i)}_{zz}(r,z)2\pi r\text{ d } r\), which results from the distribution of the normal stresses \(\sigma ^{(i)}_{zz}(r,z)\) over the same cross-sectional area \(A^{(i)}\):

$$\begin{aligned} \varSigma ^{(i)}_{zz}(z) = \dfrac{1}{A^{(i)}} \int \limits _{r^{(i-1)}}^{r^{(i)}}\sigma ^{(i)}_{zz}(r,z)2\pi r\text{ d } r. \end{aligned}$$

(16)

In order to proceed, we need to find expressions for both the average normal stresses \(\varSigma ^{(1)}_{zz}(z)\) and \(\varSigma ^{(2)}_{zz}(z)\) in terms of \(\varSigma ^{(0)}_{zz}(z)\).

With the help of (1) and (7) and after calculating the integral in (16), we obtain the following expression for the average normal stresses:

$$\begin{aligned} \varSigma ^{(i)}_{z}(z) = \sigma ^{(i)}_{z}(r^{(i-1)},z) + H_1^{(i)} \dfrac{\partial a^{(i)}(z)}{\partial z}+ H_2^{(i)} \dfrac{\partial b^{(i)}(z)}{\partial z}, \end{aligned}$$

(17)

where we have collected the geometric and the material parameters of the component \(\varOmega ^{(i)}\) in the two constants

$$\begin{aligned} H_1^{(i)}= & {} \dfrac{2\pi }{A^{(i)}} \dfrac{E^{(i)}}{\mu ^{(i)}} \Bigg [\dfrac{\left[ r^{(i)}\right] ^2}{2}\ln \left( \dfrac{r^{(i)}}{r^{(i-1)}}\right) \dfrac{\left[ r^{(i-1)}\right] ^2-\left[ r^{(i)}\right] ^2}{4}\Bigg ], \end{aligned}$$

(18a)

$$\begin{aligned} H_2^{(i)}= & {} \dfrac{2\pi }{A^{(i)}} \dfrac{E^{(i)}}{\mu ^{(i)}}\dfrac{1}{8}\left( \left[ r^{(i)}\right] ^2-\left[ r^{(i-1)}\right] ^2\right) ^2. \end{aligned}$$

(18b)

In the following parts, we derive the expressions for the average normal stresses of the interphase and the matrix.

Average normal stress \(\varSigma ^{(1)}_{zz}(z)\) in the interphase After substitution of \(i=1\) into (17), we obtain the average normal stress for the interphase \(\varOmega ^{(1)}\) in the form

$$\begin{aligned} \varSigma ^{(1)}_{zz}(z)= & {} D_1^{(1)}\varSigma ^{(0)}_{zz}(z) +D_2^{(1)}(z)\dfrac{\partial \varSigma ^{(0)}_{zz}(z)}{\partial z}+ D_3^{(1)}(z)\dfrac{\partial ^2 \varSigma ^{(0)}_{zz}(z)}{\partial z^2} +D_4^{(1)}\dfrac{\partial ^2 \varSigma ^{(2)}_{zz}(z)}{\partial z^2}, \end{aligned}$$

(19)

where we have applied the abbreviations

$$\begin{aligned}&D_1^{(1)} =\dfrac{E^{(1)}}{E^{(0)}}, \end{aligned}$$

(20a)

$$\begin{aligned}&D_2^{(1)}(z) =-\,E^{(1)}\dfrac{r^{(0)}}{2}\dfrac{\partial \gamma ^{(0,1)}(z)}{\partial z},\end{aligned}$$

(20b)

$$\begin{aligned}&D_3^{(1)}(z) = -\,E^{(1)}\dfrac{r^{(0)}}{2}\gamma ^{(0,1)}(z)+ C_1^{(1)}H_1^{(1)}+C_3^{(1)}H_2^{(1)},\end{aligned}$$

(20c)

$$\begin{aligned}&D_4^{(1)} =C_2^{(1)}H_1^{(1)}+C_4^{(1)}H_2^{(1)}. \end{aligned}$$

(20d)

Note that \(D_2^{(1)}(z)\) and \(D_3^{(1)}(z)\) depend on \(\gamma ^{(0,1)}(z)\), and therefore, they may be functions of z if axially varying bonding conditions are taken into account.

Average normal stress \(\varSigma ^{(2)}_{zz}(z)\) in the matrix: After substitution of \(i=2\) into (17), we obtain the average normal stress for the interphase \(\varOmega ^{(2)}\) in the form

$$\begin{aligned}&\varSigma ^{(2)}_{z}(z) = D_1^{(2)}\varSigma ^{(0)}_{z}(z)+D_2^{(2)}(z)\dfrac{\partial \varSigma ^{(0)}_{z}(z)}{\partial z}+ D_3^{(2)}(z) \dfrac{\partial ^2 \varSigma ^{(0)}_{z}(z)}{\partial z^2} \nonumber \\&\quad \qquad \qquad \quad D_4^{(2)}(z)\dfrac{\partial \varSigma ^{(2)}_{z}(z)}{\partial z}+ D_5^{(2)}(z) \dfrac{\partial ^2 \varSigma ^{(2)}_{z}(z)}{\partial z^2}, \end{aligned}$$

(21)

where

$$\begin{aligned}&D_1^{(2)}=\dfrac{E^{(2)}}{E^{(0)}}, \end{aligned}$$

(22a)

$$\begin{aligned}&D_2^{(2)}(z)=-\,E^{(2)}\dfrac{r^{(0)}}{2}\dfrac{\partial \gamma ^{(0,1)}(z)}{\partial z},\end{aligned}$$

(22b)

$$\begin{aligned}&D_3^{(2)}(z)=-\,E^{(2)}\dfrac{r^{(0)}}{2}\gamma ^{(0,1)}(z) + \dfrac{E^{(2)}}{\mu ^{(1)}} \ln \left( \dfrac{r^{(1)}}{r^{(0)}}\right) C_1^{(1)}\quad + \dfrac{E^{(2)}}{\mu ^{(1)}}\dfrac{\left[ r^{(1)}\right] ^2-\left[ r^{(0)}\right] ^2}{2}C_3^{(1)},\end{aligned}$$

(22c)

$$\begin{aligned}&D_4^{(2)}(z)=\dfrac{\left[ r^{(2)}\right] ^2-\left[ r^{(1)}\right] ^2}{2r^{(1)}} E^{(2)}\dfrac{\partial \gamma ^{(1,2)}(z)}{\partial z},\end{aligned}$$

(22d)

$$\begin{aligned}&D_5^{(2)}(z)= \dfrac{\left[ r^{(2)}\right] ^2-\left[ r^{(1)}\right] ^2}{2r^{(1)}} E^{(2)}\gamma ^{(1,2)}(z) + \dfrac{E^{(2)}}{\mu ^{(1)}} \ln \left( \dfrac{r^{(1)}}{r^{(0)}}\right) \nonumber \\&\quad \,\,\,\qquad \qquad C_2^{(1)} + \dfrac{E^{(2)}}{\mu ^{(1)}}\dfrac{\left[ r^{(1)}\right] ^2-\left[ r^{(0)}\right] ^2}{2}C_4^{(1)} + H_1^{(2)}C_1^{(2)}+H_2^{(2)}C_3^{(2)}. \end{aligned}$$

(22e)

Here, \(D_2^{(2)}(z)\) and \(D_3^{(2)}(z)\) may be functions of z due to their dependence on the bonding parameter \(\gamma ^{(0,1)}(z)\), and \(D_4^{(2)}(z)\) and \(D_5^{(2)}(z)\) may be functions of z due to their dependence on the bonding parameter \(\gamma ^{(1,2)}(z)\).

Coupled system of ordinary differential equations in terms of the average normal stresses

The second derivatives of (14) with respect to z and the expressions for the average normal stresses in (19) and (21) for the interphase and for the matrix form a system of three ordinary differential equations of the second order in terms of average normal stresses in the three constituents,

$$\begin{aligned} \dfrac{\partial ^2\varSigma ^{(0)}_{zz}}{\partial z^2}= & {} -\,\dfrac{\alpha _5\beta _2 - \alpha _7\beta _1}{\alpha _4\alpha _7 - \alpha _5\alpha _6}, \end{aligned}$$

(23a)

$$\begin{aligned} \dfrac{\partial ^2\varSigma ^{(1)}_{zz}}{\partial z^2}= & {} \dfrac{ \left[ \alpha _1 \alpha _5 - \alpha _3 \alpha _4\right] \beta _2 + \left[ \alpha _3 \alpha _6 - \alpha _1 \alpha _7\right] \beta _1}{\alpha _2 \left[ \alpha _4 \alpha _7 - \alpha _5 \alpha _6\right] },\end{aligned}$$

(23b)

$$\begin{aligned} \dfrac{\partial ^2\varSigma ^{(2)}_{zz}}{\partial z^2}= & {} \dfrac{\alpha _4 \beta _2 - \alpha _6 \beta _1}{\alpha _4 \alpha _7 - \alpha _5 \alpha _6}, \end{aligned}$$

(23c)

where we have used the abbreviations

$$\begin{aligned} \alpha _1= & {} A^{(0)},\quad \alpha _2=A^{(1)},\quad \alpha _3=A^{(2)},\nonumber \\ \alpha _4= & {} D_3^{(1)},\quad \alpha _5=D_4^{(1)},\quad \alpha _6=D_3^{(2)},\nonumber \\ \alpha _7= & {} D_5^{(2)}, \end{aligned}$$

(24)

and

$$\begin{aligned} \beta _1= & {} \varSigma ^{(1)}_{zz}(z) -D_1^{(1)} \varSigma ^{(0)}_{zz}(z) -D_2^{(1)} \dfrac{\partial \varSigma ^{(0)}_{zz}(z)}{\partial z},\nonumber \\ \beta _2= & {} \varSigma ^{(2)}_{z}(z) - D_1^{(2)}\varSigma ^{(0)}_{z}(z) -D_2^{(2)} \dfrac{\partial \varSigma ^{(0)}_{z}(z)}{\partial z} - D_4^{(2)}\dfrac{\partial \varSigma ^{(2)}_{z}(z)}{\partial z}. \end{aligned}$$

(25)

Together with the set of three two-point boundary conditions at \(z=0\) and \(z=L\) for the average normal stresses \(\varSigma ^{(0)}_{zz}(z)\), \(\varSigma ^{(1)}_{zz}(z)\), and \(\varSigma ^{(2)}_{zz}(z)\) in (15), the system of Eqs. (23) provides a relation between the applied force \(F^{(0)}\) and the stress distribution in the composite. It might be difficult to find an analytic solution to this problem, so that numerical approaches may be used in order to approximate the solution. For example, "bvp4c" in MATLAB is a finite difference code that implements the three-stage Lobatto IIIa formula [22].

Comparison to known results

Special cases of our here derived fiber pull-out problem have been studied in different articles. Consider a fiber \(\varOmega ^{(0)}\) in perfect bonding (\(\gamma ^{(0,2)}=0\)) with the matrix \(\varOmega ^{(2)}\) in the absence of an interphase. Figure 2 compares the present results from this article to the results by Kim et al. [33] for two fiber lengths \(L=50r^{(0)}\), and \(L=100r^{(0)}\). We take the ratios \(r^{(2)}/r^{(0)}=10\) for the radii and \(E^{(0)}/E^{(2)}=100\) for the Young's moduli, and the values \(\nu ^{(0)}=\nu ^{(2)}=1/3\) for the Poisson's ratios. Figure 2a depicts the normalized average normal stresses in the fibers, and Fig. 2b depicts the normalized interfacial shear stresses between the fiber and the matrix. The results are closer together when the fiber length increases. The present results show higher shear stresses at the ends of the fibers.

Fig. 2
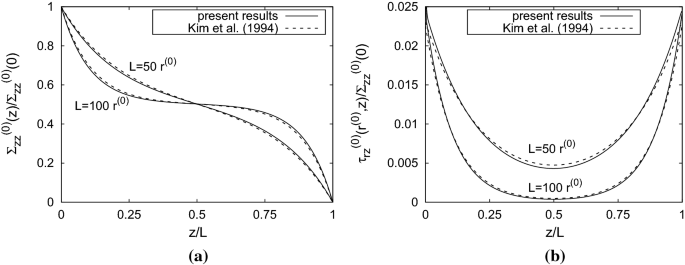
figure 2

Comparison of the results from this article to the results by Kim et al. [33] for two fiber lengths \(L=50r^{(0)}\), and \(L=100r^{(0)}\). We take the ratios \(r^{(2)}/r^{(0)}=10\) for the radii and \(E^{(0)}/E^{(2)}=100\) for the Young's moduli, and the values \(\nu ^{(0)}=\nu ^{(2)}=1/3\) for the Poisson's ratios. Figure 2a depicts the normalized average normal stresses in the fibers. Figure 2b depicts the normalized interfacial shear stresses between the fiber and the matrix

Full size image

Numerical examples

In order to illustrate the impact of the bonding on the stress distribution of the cylinder model, we consider some numerical examples, in which we take the material to be elastic with time-independent mechanical properties.

Consider a steel fiber \(\varOmega ^{(0)}\) (Tenga et al. [44]: Young's modulus of \(E^{(0)}=200\,\text{ GPa }\), shear modulus of \(G^{(0)}=76.92\,\text{ GPa }\), Poisson's ratio of \(\nu ^{(0)}=\frac{1}{3}\)) with the length \(L=10^{-2}\,\text{ m }\) in a bulk polystyrene matrix \(\varOmega ^{(2)}\) (approximated from Cheng et al. [11]: \(E^{(2)}=2.1\,\text{ GPa }\), \(\nu =0.33\), \(G^{(2)}=\frac{E^{(2)}}{2[1+\nu ]}\approx 1.58\,\text{ GPa }\)). The fiber is loaded by a force \(F^{(0)}=0.1\,\text{ N }\). The radii of the fiber and the cylinder model are \(r^{(0)} = 10^{-4}\,\text{ m }\) and \(r^{(2)} = 10^{-3}\,\text{ m }\).

Fig. 3
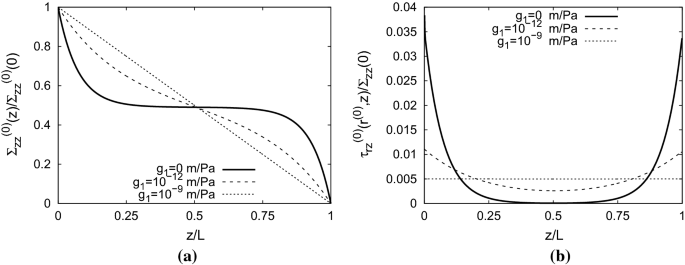
figure 3

Stress distribution in a fiber–matrix composite for the constant bonding parameter (26): a The normalized average normal stresses in the fiber with the axial location. b The normalized shear stresses at the interface between the fiber and the matrix

Full size image

Constant bonding between the fiber and the matrix:   Consider a fiber \(\varOmega ^{(0)}\) and the matrix \(\varOmega ^{(2)}\) in the absence of any interphase \(\varOmega ^{(1)}\). Let us assume that bonding between the fiber \(\varOmega ^{(0)}\) and the matrix \(\varOmega ^{(2)}\) is described by the constant bonding parameter

$$\begin{aligned} \gamma ^{(0,2)}(z)=g_1 \end{aligned}$$

(26)

in the units of \(\frac{\text{ m }}{\text{ Pa }}\). Figure 3 shows the stress distribution in the composite for \(g_1=0\) (perfect bonding), \(g_1=10^{-12}\frac{\text{ m }}{\text{ Pa }}\), and \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\). Figure 3a depicts the normalized average normal stresses \(\varSigma _{zz}^{(0)}(z)/\varSigma _{zz}^{(0)}(0)\) in the fiber with the axial location. For large values of \(g_1\), the stress distribution approximates a diagonal line. Figure 3b depicts the distribution of the normalized shear stresses \(\tau ^{(0)}(r^{(0)},z)/\varSigma _{zz}^{(0)}(0)\) at the interface between the fiber and the matrix. These shear stresses have a minimum near \(z=L/2\) and larger value at the ends of the fiber. For large values of \(g_1\), the shear stress distribution approximates a horizontal line. In analytic solutions, the shear stresses \(\tau ^{(0)}(r^{(0)},z)\) will have singularities at \(z=0\), which will lead to debonding, because the infinite stress will definitely lead to a partial local damage of the interface. This singularity can be removed by introducing a thin interphase between the fiber and the matrix [35].

Fig. 4
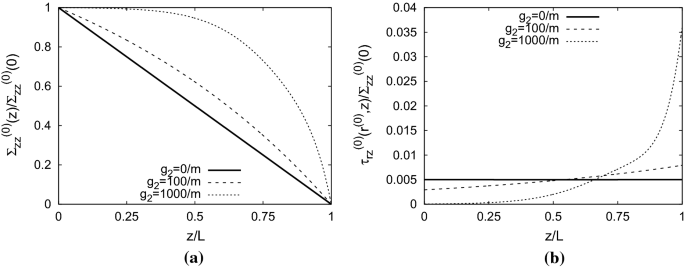
figure 4

Stress distribution in a fiber–matrix composite for the axially varying bonding parameter (27) for \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\) and different values of \(g_2\): a The normalized average normal stresses in the fiber with the axial location. b The normalized shear stresses at the interface between the fiber and the matrix

Full size image

Axially varying bonding between the fiber and the matrix   Let us assume that bonding may be weak near \(z=0\) and stronger at the other fiber end near \(z=L\). Such varying bonding may be caused, for example, by diffusion of moisture into the interface or material degradation starting from the surface at \(z=0\). Bonding between the fiber and the matrix is considered in the form

$$\begin{aligned} \gamma ^{(0,2)}(z)=g_1e^{-g_2z}, \end{aligned}$$

(27)

where \(g_1\) is a parameter in the units of \(\frac{\text{ m }}{\text{ Pa }}\), and \(g_2\) is parameter in the units of \(\text{ m }^{-1}\) that quantifies the change of the bonding with the axial location. Figure 4 shows the stress distribution in a fiber–matrix composite for the axially varying bonding parameter (27) for \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\) in combination with \(g_2=0\) (constant bonding), \(g_2=100\frac{1}{\text{ m }}\), and \(g_2=1000\frac{1}{\text{ m }}\). Figure 4a shows the normalized average normal stresses in the fiber with the axial location, and Fig. 4b shows the normalized shear stresses at the interface between the fiber and the matrix.

The results show that increasing \(g_2\) increases the average normal stress of the fiber near \(z=0\), while the interfacial shear stresses become larger near \(z=L\).

Fig. 5
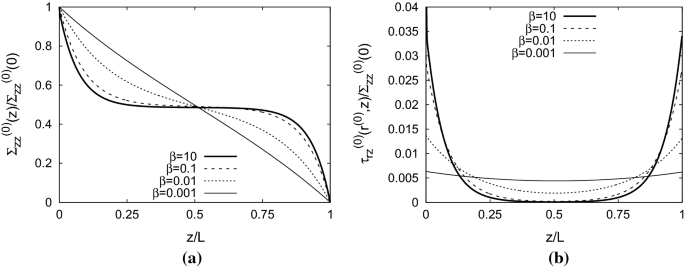
figure 5

Stress distribution in a fiber–interphase–matrix composite for different values of the proportionality constant \(\beta \) in (28): a The normalized average normal stresses in the fiber with the axial location. b The normalized shear stresses at the interface between the fiber and the matrix

Full size image

Interphase between the fiber and the matrix   Consider an interphase \(\varOmega ^{(1)}\) with the outer radius \(r^{(1)}=1.1\times 10^{-4}\text{ m }\) between the fiber \(\varOmega ^{(0)}\) and the matrix \(\varOmega ^{(2)}\), where bonding between these material is taken to be perfect, \(\gamma ^{(0,1)}=\gamma ^{(1,2)}=0\). This interphase may be a coupling agent or a modeling material that shall simulate bonding between the fiber and the matrix. Let us assume that

$$\begin{aligned} E^{(1)}=\beta E^{(2)}, \qquad \mu ^{(1)}=\beta \mu ^{(2)}, \end{aligned}$$

(28)

where \(\beta \) is a proportionality constant that relates the material parameters of the interphase \(\varOmega ^{(1)}\) to those of the matrix \(\varOmega ^{(2)}\). Figure 5 shows stress distribution in a fiber–interphase–matrix composite for different values of the proportionality constant \(\beta \) in (28).

If we compare the results from Fig. 5 to the results of Fig. 3 for a constant and imperfect bonding, then we can see that the distribution of the average normal and shear stresses have some similarities. If we compare the stress distribution for imperfect bonding by the spring-layer model and by a modeling interphase, then we can determine some geometric and mechanical properties for the interphase that simulates imperfect bonding, for example for application where imperfect bonding cannot be explicitly modeled by boundary conditions in the interface between two constituents (see, e.g., Andrianov et al. [5]).

A soft interphase between the loaded fiber and the matrix reduces the high values of shear stresses at the end of the fibers (also see, e.g., Lenci and Menditto [35] and Andrianov et al. [2]).

Viscoelastic behavior

In fiber-reinforced composites, some constituents may consist of polymers, which reveal a time-dependent mechanical behavior. Then, even for a constant pull-out force \(F^{(0)}\) the distribution of the stresses will vary with time.

Let us now assume that a constituent of the composite shows a viscoelastic behavior. In the modeling of viscoelastic materials, the elastic behavior of the material can be described by spring elements, and the viscous behavior in terms of dashpot elements.

The stress tensor \(\varvec{\sigma }^{(i)}\) and the strain tensor \(\varvec{\varepsilon }^{(i)}\) of constituent \(\varOmega ^{(i)}\) may be decomposed into hydrostatic parts, namely \(\bar{\varvec{\sigma }}^{(i)}=\text{ diag }(\bar{\sigma }^{(i)},\bar{\sigma }^{(i)},\bar{\sigma }^{(i)})\) and \(\bar{\varvec{\varepsilon }}^{(i)}=\text{ diag }(\bar{\varepsilon }^{(i)},\bar{\varepsilon }^{(i)},\bar{\varepsilon }^{(i)})\), where \(\bar{\sigma }^{(i)}=\frac{1}{3}\left[ \sigma _{11}+\sigma _{22}+\sigma _{33}\right] \) and \(\bar{\varepsilon }^{(i)}=\frac{1}{3}\left[ \varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}\right] \), and into deviatoric parts \(\varvec{\tau }^{(i)}\) and \(\varvec{\epsilon }^{(i)}\),

$$\begin{aligned} \varvec{\sigma }^{(i)}=\bar{\varvec{\sigma }}^{(i)}+\varvec{\tau }^{(i)},\qquad \varvec{\varepsilon }^{(i)}=\bar{\varvec{\varepsilon }}^{(i)}+\varvec{\epsilon }^{(i)}. \end{aligned}$$

(29)

Then, the elements \(\bar{\sigma }^{(i)}\) and \(\bar{\varepsilon }^{(i)}\) of the hydrostatic tensors and the elements \(\tau _{ij}^{(i)}\) and \(\epsilon _{ij}\) of the deviatoric tensors can be related via

$$\begin{aligned} \sum _{j=0}^{j_\mathrm{max}}\bar{p}_{j}^{(i)}\dfrac{\partial ^j \bar{\sigma }^{(i)}}{\partial t^j}= & {} \sum _{k=0}^{k_\mathrm{max}}\bar{q}_{k}^{(i)}\dfrac{\partial ^k \bar{\varepsilon }^{(i)}}{\partial t^k},\qquad \bar{p}_{0}^{(i)} = 1, \end{aligned}$$

(30a)

$$\begin{aligned} \sum _{j=0}^{j_\mathrm{max}}{p}_{j}^{(i)}\dfrac{\partial ^j \tau _{lm}^{(i)}}{\partial t^j}= & {} \sum _{k=0}^{k_\mathrm{max}}{q}_{k}^{(i)}\dfrac{\partial ^k {\epsilon }_{lm}^{(i)}}{\partial t^k} ,\qquad {q}_{0}^{(i)} = 1. \end{aligned}$$

(30b)

If \(j_\mathrm{max}=k_\mathrm{max}=0\), then the material is elastic and \(\bar{p}_{0}^{(i)}=3K^{(i)}\) and \({p}_{0}^{(i)}=2\mu ^{(i)}\), where \(K^{(i)}\) and \(\mu ^{(i)}\) are the bulk modulus and the shear modulus of constituent \(\varOmega ^{(i)}\).

Let us introduce the differential operators

$$\begin{aligned} \bar{\mathcal {P}}= & {} \sum _{j=0}^{j_\mathrm{max}}\bar{p}_{j}^{(i)}\dfrac{\partial ^j }{\partial t^j}, \qquad \bar{\mathcal {Q}} = \sum _{k=0}^{k_\mathrm{max}}\bar{q}_{k}^{(i)}\dfrac{\partial ^k }{\partial t^k}, \end{aligned}$$

(31a)

$$\begin{aligned} {\mathcal {P}}= & {} \sum _{j=0}^{j_\mathrm{max}}{p}_{j}^{(i)}\dfrac{\partial ^j }{\partial t^j}, \qquad {\mathcal {Q}} = \sum _{k=0}^{k_\mathrm{max}}{q}_{k}^{(i)}\dfrac{\partial ^k }{\partial t^k}. \end{aligned}$$

(31b)

The relation between the applied loading and the deformation of the composite at time t depends on the past loading and deformation history. Let us take the material to be to undeformed and to be unloaded at time \(t<0\), and at \(t>0\) suddenly subjected to an axial fiber load \(F^{(0)}_0\), which remains constant,

$$\begin{aligned} F^{(0)}(t)=H(t)F^{(0)}_0, \end{aligned}$$

(32)

where H(t) is the Heaviside step function.

Laplace transform of the viscoelastic problem

A direct treatment of the viscoelastic problem in the time domain is often complicated. In order to simplify the treatment, we transfer the problem from time t domain into an s domain by the Laplace transform. Consider a function f(t) of time t. Then, the Laplace transform \(\hat{f}(s)\) of the original time t-dependent function f(t) into the domain s is obtained via

$$\begin{aligned} \hat{f}(s)=\mathcal {L}\left( f(t)\right) =\int _{0}^{\infty }f(t)e^{-st}\text{ d }t. \end{aligned}$$

(33)

The Laplace transforms of the derivatives of f(t) with respect to time t then become

$$\begin{aligned} \displaystyle \int _{0}^{\infty } \dfrac{\text{ d }^N f(t)}{\text{ d } t^N} e^{-st}\text{ d }t = \displaystyle s^N\hat{f}(s)-\sum _{n=1}^{N}s^{n-1} \left. \dfrac{\text{ d }^{N-n} f(t)}{\text{ d } t^{N-n}} \right| _{t=0}. \end{aligned}$$

(34)

Let us now assume that the function f(t) has a singularity for \(t=0\), so that f(t) as well as its derivatives with respect to t are equal to zero for \(t<0\). Then, if we take \(t=0^-\) as the lower integration limit in (34), the right side reduces to \(s^N\hat{f}(s)\) (see [16]).

In this s domain, the step force (32) becomes

$$\begin{aligned} \mathcal {L}\left( {F}^{(0)}(t)\right) ={F}^{(0)}_0/s. \end{aligned}$$

(35)

Then, for the load application at \(t=0^+\), the Laplace transform of the differential operators in (31) becomes

$$\begin{aligned} \hat{\bar{\mathcal {P}}}(s)= & {} \sum _{j=0}^{j_\mathrm{max}}{\bar{p}}_{j}^{(i)}s^j, \qquad \hat{\bar{\mathcal {Q}}}(s) = \sum _{k=0}^{k_\mathrm{max}}\bar{q}_{k}^{(i)}s^k, \end{aligned}$$

(36a)

$$\begin{aligned} \hat{{\mathcal {P}}}(s)= & {} \sum _{j=0}^{j_\mathrm{max}}{p}_{j}^{(i)}s^j, \qquad \hat{\mathcal {Q}}(s) = \sum _{k=0}^{k_\mathrm{max}}{q}_{k}^{(i)}s^k. \end{aligned}$$

(36b)

Let \(\hat{ \bar{\sigma }}^{(i)}\) and \(\hat{ \tau }_{ij}^{(i)}\) be the Laplace transforms of the stress components \({\bar{\sigma }}^{(i)}\) and \({\tau }_{ij}^{(i)}\), and \(\hat{ \bar{\varepsilon }}^{(i)}\) and \(\hat{\epsilon }_{ij}^{(i)}\) be the Laplace transforms of the strain components \({ \bar{\varepsilon }}^{(i)}\) and \({\epsilon }_{ij}^{(i)}\). Then, with the help of (36) the Laplace transforms of (30) become

$$\begin{aligned} \hat{\bar{\mathcal {P}}}(s)\hat{ \bar{\sigma }}^{(i)}= & {} \hat{\bar{\mathcal {Q}}}(s)\hat{ \bar{\varepsilon }}^{(i)}, \end{aligned}$$

(37a)

$$\begin{aligned} {\hat{\mathcal {P}}}(s)\hat{ \tau }_{lm}^{(i)}= & {} {\hat{\mathcal {Q}}}(s)\hat{\epsilon }_{lm}^{(i)}. \end{aligned}$$

(37b)

It might be difficult to find the inverse Laplace transform, and different theorems and methods have been found in order to find or to approximate the inverse. For example, the Gaver–Stehfest algorithm (see Gaver [19] and Stehfest [43]) is a one-dimensional algorithm which does not use complex numbers (see, e.g., [8]).

The initial-value theorem and the final-value theorem, for example, allow to identify some properties of a function f(t) for the time of load application \(t=0\) and for \(t\rightarrow \infty \) (see, e.g., Doetsch [14]),

$$\begin{aligned} \lim _{t\rightarrow 0}f(t)= & {} \lim _{t\rightarrow \infty }s\hat{f}(s), \end{aligned}$$

(38a)

$$\begin{aligned} \lim _{t\rightarrow \infty }f(t)= & {} \lim _{t\rightarrow 0}s\hat{f}(s). \end{aligned}$$

(38b)

In combination with (34), further properties of f(t) for \(t=0\) and \(t\rightarrow \infty \) can be identified.

The elastic–viscoelastic correspondence principle

The elastic–viscoelastic correspondence principle is based on the idea that the treatment of a linear elastic problem and the Laplace transformed linear viscoelastic problem shows certain analogies (see, e.g., the classical book by Flügge [16]). Let us make the following substitutions for the bulk modulus \(K^{(i)}\) and the shear modulus \(\mu ^{(i)}\) (see [16])

$$\begin{aligned} K^{(i)} \rightarrow \dfrac{1}{3}\dfrac{\hat{\bar{\mathcal {Q}}}(s)}{\hat{\bar{\mathcal {P}}}(s)}, \qquad \mu ^{(i)} \rightarrow \dfrac{1}{2}\dfrac{{\hat{\mathcal {Q}}}(s)}{{\hat{\mathcal {P}}}(s)}. \end{aligned}$$

(39)

In our modeling of the pulled-out fiber problem, the mechanical behavior of the constituents is described in terms of the shear modulus and the Young's modulus \(E^{(i)}=\frac{9K^{(i)}\mu ^{(i)}}{3K^{(i)}+\mu ^{(i)}}\), for which the substitution

$$\begin{aligned} E^{(i)}\rightarrow \dfrac{3{\hat{\mathcal {Q}}}(s)\hat{\bar{\mathcal {Q}}}(s)}{2{\hat{\mathcal {P}}}(s)\hat{\bar{\mathcal {Q}}}(s)+\hat{\bar{\mathcal {P}}}(s){\hat{\mathcal {Q}}}(s)} \end{aligned}$$

(40)

is applied.

Numerical examples

Fig. 6
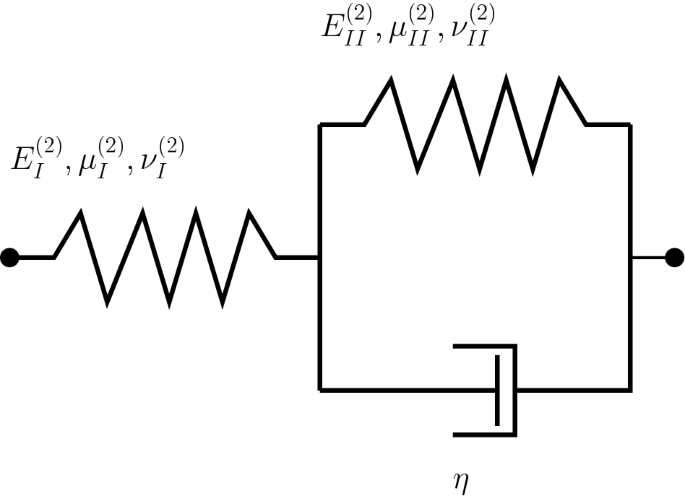
figure 6

Viscoelastic behavior described by a three-parameter standard solid: a spring with the stiffness \(E_{I}^{(2)}\) is in series to a parallel arrangement of another spring with the stiffness \(E_{II}^{(2)}\) and a dashpot

Full size image

Fig. 7
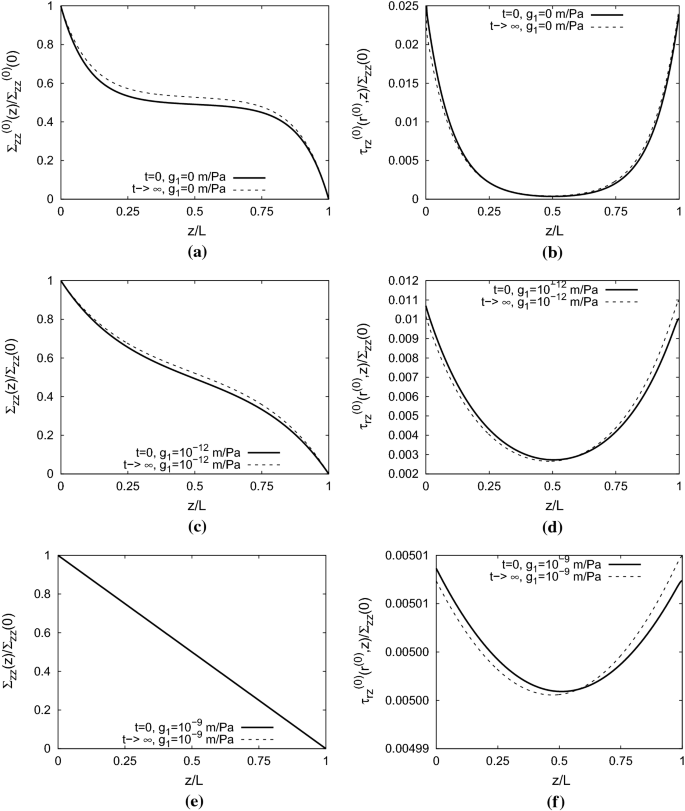
figure 7

Stress distribution in a fiber–matrix composite for the constant bonding parameter (26): The left panels a, c, e show the normalized average normal stresses in the fiber with the axial location. The right panels b, d, f show the normalized shear stresses at the interface between the fiber and the matrix. The panels a, b are for \(g_1=0\) (perfect bonding). The middle panels c, d are for \(g_1=10^{-12}\,\frac{\text{ m }}{\text{ Pa }}\). The bottom panels e, f are for \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\). The solid lines for \(t=0\) show the instantaneous response directly after load application, and the dashed lines show the response for \(t\rightarrow \infty \)

Full size image

Consider a steel fiber \(\varOmega ^{(0)}\) (same properties as in Sect. 3.5) with the length \(L=10^{-2}\,\text{ m }\) in a bulk polystyrene matrix \(\varOmega ^{(2)}\). While the mechanical behavior of the fiber is taken to have time-independent mechanical properties, the matrix is taken to be viscoelastic. As Cheng et al. [11] point out, for different purposes the volumetric part of models is elastic with time-independent behavior, while the deviatoric part is taken to be elastic. The viscoelastic behavior is modeled in terms of a three-parameter standard solid (Fig. 6), in which a spring with the elastic parameters \(E_{I}^{(2)}\), \(\mu _{I}^{(2)}\), and \(\nu _{I}^{(2)}\) is in series to a parallel arrangement of another spring with the elastic parameters \(E_{II}^{(2)}\), \(\mu _{II}^{(2)}\), and \(\nu _{II}^{(2)}\) and a dashpot with the viscosity \(\eta \). In the time domain, the viscoelastic behavior in (30) becomes

$$\begin{aligned} \bar{\sigma }^{(2)}= & {} \overbrace{ 3K^{(2)}}^{\bar{q}_{0}^{(2)}} \bar{\varepsilon }^{(2)}, \end{aligned}$$

(41a)

$$\begin{aligned} \sigma + \underbrace{\dfrac{\eta ^{(2)}}{\mu _{I}^{(2)}+\mu _{II}^{(2)}}}_{{p}_{1}^{(2)}} \dfrac{\partial \sigma }{\partial t}= & {} \underbrace{\dfrac{2\mu _{I}^{(2)}\mu _{II}^{(2)}}{\mu _{I}^{(2)}+\mu _{II}^{(2)}}}_{{q}_{0}^{(2)}}\varepsilon + \underbrace{\dfrac{2\mu _{I}^{(2)}\eta ^{(2)}}{\mu _{I}^{(2)}+\mu _{II}^{(2)}}}_{{q}_{1}^{(2)}}\dfrac{\partial \sigma }{\partial t}, \end{aligned}$$

(41b)

where the normalizations \(\bar{p}_{0}^{(2)}={p}_{1}^{(2)}=1\) have been applied, and \(K^{(2)}=\frac{E^{(2)}_I}{3[1-2\nu ^{(1)}]}\). For the stress–strain relations in (41), the Laplace transforms (42) become

$$\begin{aligned} \hat{\bar{\mathcal {P}}}(s)= & {} 1, \qquad \hat{\bar{\mathcal {Q}}}(s). = \bar{q}_{0}^{(2)}, \end{aligned}$$

(42a)

$$\begin{aligned} \hat{{\mathcal {P}}}(s)= & {} 1+{p}_{1}^{(2)}s, \qquad \hat{\mathcal {Q}}(s), = {q}_{0}^{(2)} + {q}_{1}^{(2)}s. \end{aligned}$$

(42b)

Then, the Laplace transforms of the shear modulus and the Young's modulus (see (39) and (40)) become

$$\begin{aligned}&\mu ^{(2)} \rightarrow \dfrac{1}{2}\dfrac{1+p_1^{(2)}s}{q_0^{(2)}+q_1^{(2)}s}, \end{aligned}$$

(43a)

$$\begin{aligned}&E^{(2)} \rightarrow \dfrac{9K^{(2)}\left[ q_0^{(2)}+q_1^{(2)}s\right] }{6K^{(2)}\left[ 1+p_1^{(2)}s\right] +\left[ q_0^{(2)}+q_1^{(2)}s\right] }. \end{aligned}$$

(43b)

Fig. 8
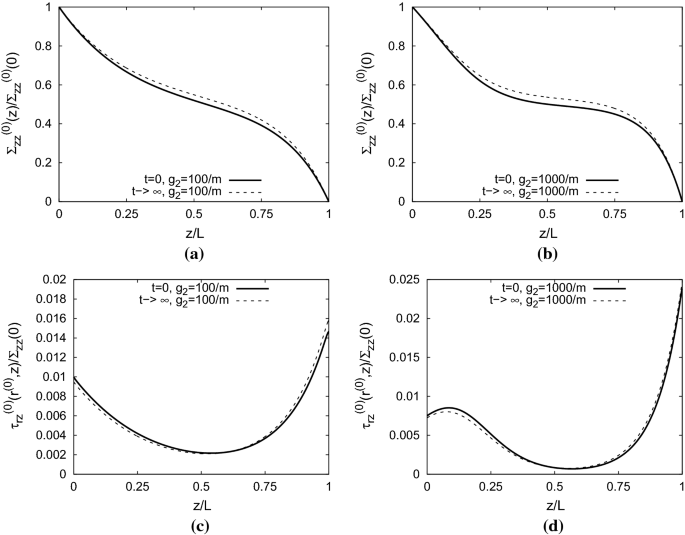
figure 8

Stress distribution in a fiber–matrix composite for the axially varying bonding parameter (27) for \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\) and different values of \(g_2\): The top panels show the normalized average normal stresses in the fiber with the axial location. The bottom panels show the normalized shear stresses at the interface between the fiber and the matrix. The left panels a, c are for \(g_2=100\,\text{ m }^{-1}\), and the right panels b, d are for \(g_2=1000\,\text{ m }^{-1}\). The solid lines for \(t=0\) show the instantaneous response directly after load application, and the dashed lines show the response for \(t\rightarrow \infty \), when the creep process has approached an end

Full size image

For these material parameters, let as take some reported values of bulk polystyrene by Cheng et al. [11]: \(E_{I}^{(2)}=2.1\,\text{ GPa }\), \(E_{II}^{(2)}=11.5\,\text{ GPa }\), and \(\eta ^{(2)}=58.2\,\text{ GPa }\). For the Poisson's ratios of \(\nu _{I}^{(2)}=\nu _{II}^{(2)}=0.33\), we obtain the shear moduli \(\mu _{I}^{(2)}=\frac{E_{I}^{(2)}}{2[1+\nu ]}=0.79\,\text{ GPa }\) and \(\mu _{II}^{(2)}=\frac{E_{II}^{(2)}}{2[1+\nu ]}=4.32\,\text{ GPa }\). For these values, the bulk modulus of the matrix becomes \(K^{(2)}=\frac{E_{I}^{(2)}}{3[1-2\nu _{I}^{(2)}]}=2.06\,\text{ GPa }\).

In the following examples, we assume that at time \(t<0\) the material is unloaded and then at \(t\ge 0\) the fiber is loaded by a constant force as described in (32).

Constant bonding between the fiber and the matrix:   As in the first example of Sect. 3.5, let us consider a fiber \(\varOmega ^{(0)}\) and the matrix \(\varOmega ^{(2)}\) in the absence of any interphase \(\varOmega ^{(1)}\). Let us assume that bonding between the fiber \(\varOmega ^{(0)}\) and the matrix \(\varOmega ^{(2)}\) is described by the constant bonding parameter \(\gamma ^{(0,2)}\) in (26). Figure 7 shows the stress distribution in a fiber–matrix composite for the constant bonding parameter (26). The left panels show the normalized average normal stresses in the fiber with the axial location. Note that because the average normal stress \(\varSigma _{zz}^{(0)}(0)\) at \(z=0\) remains constant throughout the creep process, the stresses for times \(t=0\) and \(t\rightarrow \infty \) have the same normalization. The right panels show the normalized shear stresses at the interface between the fiber and the matrix. The top panels (a) and (b) are for \(g_1=0\) (perfect bonding). The middle panels (c) and (d) are for \(g_1=10^{-12}\frac{\text{ m }}{\text{ Pa }}\). The right panels (e) and (f) are for \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\). The solid lines for \(t=0\) show the instantaneous response directly after load application, and the dashed lines show the response for \(t\rightarrow \infty \).

The top diagrams of Fig. 7 illustrate how the average normal stresses increase throughout the fiber as the supporting matrix undergoes creep, while at the fiber ends these stresses remain at \(\varSigma _{zz}^{(0)}(0)=\frac{F^{(0)}}{A^{(0)}}\) and \(\varSigma _{zz}^{(0)}(L)=0\). The differences in the fiber's average normal stresses increase and decrease for a declining quality for the bonding. The bottom diagrams show that near \(z=0\) the interfacial shear stresses decrease at \(t\rightarrow \infty \), while at the same time the interfacial shear stresses increase near \(z=L\).

Axially varying bonding between the fiber and the matrix:   Analogous to the second example of Sect. 3.5, let us assume that bonding between the fiber and the matrix varies axially, and bonding is quantified by the axially varying bonding parameter \(\gamma ^{(0,2)}(z)\) in (27) .

Figure 8 depicts the stress distribution in a fiber–matrix composite for \(g_1=10^{-9}\frac{\text{ m }}{\text{ Pa }}\) and different values of \(g_2\): The top panels show the normalized average normal stresses in the fiber with the axial location. The bottom panels show the normalized shear stresses at the interface between the fiber and the matrix. The left panels a, c are for \(g_2=100\,\text{ m }^{-1}\), and the right panels b, d are for \(g_2=1000\,\text{ m }^{-1}\). The solid lines for \(t=0\) show the instantaneous response directly after load application, and the dashed lines show the response for \(t\rightarrow \infty \).

Also in this case of axially varying bonding, the average normal stresses increase throughout the fiber as the supporting matrix undergoes creep. The interfacial shear stresses are larger at \(z=L\) in comparison with the shear stresses at \(z=L\), because of the increase in the bonding qualify for increasing values of z. Also in this example near \(z=0\), the interfacial shear stresses decrease at \(t\rightarrow \infty \), while at the same time the interfacial shear stresses increase near \(z=L\).

Conclusions

In our article, we study pull-out of a single fiber, which is embedded in a matrix. An interphase material between the fiber and the matrix is taken into account. The here presented results are based on the assumption that the outer surface is shear stress free, for example because a single-fiber pull-out problem is treated with general freedom from stresses at the outer surface of the cylinder, or because all fibers of a regular array are pulled out simultaneously.

Bonding between the different constituents is assumed to be imperfect, and the quality of bonding varies with the axial location. A modification of the spring-layer model has been applied in order to simulate bonding between the different constituents. The distribution of the average normal stresses and interfacial shear stresses has been studied for both elastic time-independent and viscoelastic problems. The herein presented results are useful for the planning of single-fiber pull-out experiments, and they may serve as references and benchmark for finite element studies. The results may also find different civil engineering applications (see, e.g., the work by Ai and Yue [1] on axially loaded piles in multilayered soils).

Different works have been devoted to simulate the pull-out of a single fiber from the composite; in the cylinder model in Fig. 1, another layer may be added with the same properties as the composite in a macroscopic level. Such an idea has been employed, for example, by Kim et al. [33] and Fu et al. [18].

While in this article bonding is described by a continuous function, this idea may be modified to piece-wise continuous functions and to boundary conditions that may change with the amount of the interfacial shear stresses.